名称がないと考えられない。名称があるとそれしか考えられない

f:id:shinzor:20210711132952p:plain

  バカバカしいと言わずに、小6の女の子の疑問に答えてみました。

先ず、「１人あたり７個」が何を表しているか考えるため、問題文の状況を図にしてみます。

 f:id:shinzor:20210711132218j:plain

　図は、７個のクッキーが５行並んでいるとも、５個のクッキーが７列並んでいるとも言えます。掛け算は「行」×「列」あるいは「列」×「行」です。簡単明瞭です。図の〇印は「行」の中だろうと、「列」の中だろうと、クッキー１個であることに変わりはありません。「列」の中では「人」に変化したりはしません。

　この「行」や「列」の長さを算数教育では「ひとつ分」と言う専門用語で呼ぶようです。「行」の長さを「ひとつ分」と考えた時には「列」の長さは「いくつ分」という分かりにくい専門用語で表します。難しいですね。

 　更に問題になのは、具体的事例では「行」や「列」に名称がない場合があることです。クッキーの例では「行」には「人」という名称があるため、「行」の長さは「一人分のクッキーの個数」と言うことができます。ところが、「列」には名称がつけられていませんので「列」の長さを簡潔に表現するのが難しくなります。

 　その結果、「１列あたり５個」の「列」に問題文にある「個」を機械的に当てはめたのでしょう。そうすると問題文に残っているのは「人」だけなので、「１個あたり５人」となってしまうわけです。今の小学校は、小6の女の子だけでなく、小学校の先生や東大卒の人ですら混乱しそうな教え方をしているんですね。私が子供の頃は簡単でしたが。

   人間の思考は言葉に相当、制限されます。名称のない「列」は考えることができなくなり、名称のある「人」しか考えられなくなります。混乱を防ぐには、「ひとつ当たり」などという言葉は一旦忘れて、行列の図を思い浮かべれば済みます。高度な数学になると、日常用語に相当するものがない専門用語が出てきます。その概念をイメージするのは私のような凡人には困難です。しかし、そのような概念を作り出した数学の天才は、イメージが頭の中に先にあるようで、後からそれに名称を付けているのではないでしょうか。ならば、そんなイメージのない凡人が言葉をいくら見ていてもなにも理解できません。

　クッキーの問題でも「列」に名称を付けることはできます。例えば、一人に配ったクッキーにNo.1から7までナンバーを付ければ、「列」は「ナンバー」になり、「列の長さ」は「ナンバー当たりのクッキー個数」になります。

　「列」に名称がつけられていない代表例に「単価」×「数量」＝「価格」があります。この場合は、「行」には「数量」という名称があり、「１行当たり価格」を意味する「行」の長さに「単価」という名称があります。しかし「列」には名称がなく、「１列当たり価格」を意味する「行」長さの名称もありません。

　「速さ」×「時間」＝「距離」も同様です。「行」には「時間」という名称があり」、「１行あたり距離」を意味する「行」の長さに「速さ」という名称があります。しかし、「列」や「列」の長さは名無しです。「数量」や「時間」も「ひとつ当たり」とすることもできますが、言葉での表現がややこしくなります。

　しかし、行列のイメージがあれば、単純かつ自由自在に考えることができます。天才的な数学者でない普通の子供でもできます。言葉（名称）は思考の助けになる便利なものですが、言葉（名称）がないものは無視してしまいがちになる弊害もあるのじゃないでしょうか。

 

目先のことしか考えられない

  予防接種法は平成６年改正で、義務接種から勧奨接種になりました。その背景は次のように説明してあります。

予防接種制度 について

・ 公衆衛生や生活水準の向上により、予防接種に対する国民の考え方は、各個人の

疾病予防のために接種を行い、自らの健康の保持増進を図るという考え方へ変化。

・ 予防接種制度については、国民全体の免疫水準を維持し、これにより全国的又は

広域的な疾病の発生を予防するという面とともに、個人の健康の保持増進を図るとい

う面を重視した制度とすることが必要。

 　それらしく書いてありますが、端的に言えば、行政責任の回避です。「全国的又は広域的な疾病の発生を予防する」から「個人の健康の保持増進を図る」という変化は、行政が責任を持つ社会防衛は止めて、「個人の健康の問題にしたので自己責任でやってね」と言っているわけです。リンク先の資料にも書いてあるように「種痘後脳炎などの副反応が社会的に大きな問題」となったのが直接的原因で、決定的なのは裁判で厚労省の責任が問われたことです。有罪ともなれば、止めたくもなろうというものです。ある意味で、国民の希望に応えたともいえます。

 　通常、病気の治療は義務でもないし、医師から強制されることはありません。あくまで患者本人の自由意志で決定します。予防接種もそれと同じ扱いになったわけです。予防接種に伴う被害が生じても、通常の医療裁判と同じように、接種した医師と接種された人の間で解決することになり、国は直接関与しない立場になったわけです。一応、健康被害救済制度はありますが、国の責任は大幅に軽減されました。

 　それに対して、従来の予防接種の義務は、個人の予防ではなく、社会への感染の蔓延を防止するという公共目的で行われていました。接種義務は憲法が保証する国民の権利を制限しますので、「公共の福祉」という大義が必要ですし、国しか出来ない仕事です。

　国民の権利を制限というと恐ろしい印象を受けますが、大抵の法律は普通に行っています。例えば、建築基準法は、本来自由に作ってよいはずの個人の敷地内の私有財産について、あれこれ制限します。制限するのは、隣の家が日陰になるとか、出火して延焼すれば、大迷惑だからです。このような問題も、当事者同士で話し合って解決してもらい、国は口出しないというやり方もありますが、関係者が膨大になり、被害と原因の因果関係もあいまいで経験的に巧くいかないとわかっています。個々の解決に任せると、いわゆる合成の誤謬という現象が起こる場合があり、都市問題はその一例で、大抵、スラム化します。

　国防や警察も同様ですが、国民の権利を制限するので評判が悪くなるのが宿命です。規制行政は、しばしば杓子定規な運用もあって苦情が殺到します。それでも、規制を止める例は少ないですが、稀に「そこまで文句言うなら、勝手にしろ」とさじを投げることがあります。記憶にあるのが公共工事の予定価格の事前公表です。予定価格の漏洩が問題になると、秘密保持という行政責任を放棄して予定価格の事前公表をしてしまった自治体がありました。公表した情報の漏洩責任を問われる心配は全くありませんからね。

　予防接種義務の廃止もその数少ない例の一つです。廃止したのは予防接種に害があるからではありません。義務は廃止しましたが、「勧奨」はしているんですからね。「勧奨」でも、接種は行わたので、それでもいいのかしれません。強制しないで済むならそれにこしたことはありません。

 　ただ、HPVワクチンに関しては、「勧奨」はしても「積極的勧奨」を止めたため結構な被害がこれから出てくると予想されています。「がん」は健康被害がでるまで時間がかかるので、予防の効果を実感できないのが大きいのかもしれません。

 　HPVワクチン同様に新型コロナワクチンでも反ワクチンが喧しいです。しかし、がんと違ってすぐに発症する病気では、効果が見えやすいせいか、HPVワクチンみたいな惨状にならずに済んでいます。遠い将来のことは考えられなくても、目先のことは気になるんですね。私も将棋の三手が読めません。

構造力学クイズー変形能力

　ちょっとしたクイズです。構造力学を習った人なら基本中の基本問題で、専門外でも、高校物理の知識があれば解ける問題です。必要な知識は力のつり合いとフックの法則ぐらいです。

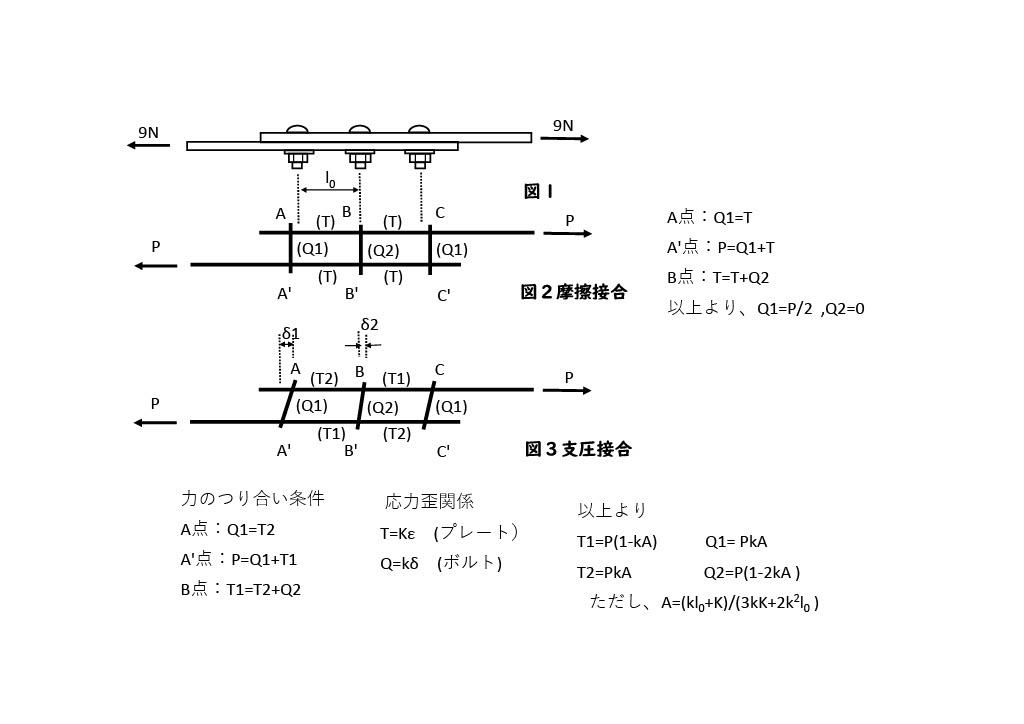
　図１のようにプレート（鉄板）を３本のボルトで接合して、９ニュートンの力で引っ張れば、それぞれのボルトに働くせん断力は、いくらでしょうか？

　単純に９/３＝３ニュートンと計算してよいのかというクイズです。実用的な計算ではそうしてよいことになっていますが、厳密にはどうなのでしょうか。実は、条件不足でこれだけでは答えは分かりません。ボルトには、ボルトの軸の側面とプレートの支圧で力を伝える普通ボルトと、強烈な力で締め付けてプレート同士を密着させその摩擦力で力を伝える高力ボルトがあり、答えが違ってきます。

 　考えやすい摩擦接合の高力ボルトについて先ず考えてみます。図２において、摩擦接合なのでボルト位置での上下のプレートにズレは生じません。そのため上下プレートのボルト間の伸びは同じになります。また、対称性から、１枚のプレートのAB間とBC間の伸びも同じになり、引張応力Tも同じになります。このことから、B点の力のつり合いより、中央ボルトの剪断力（摩擦力）は0です。３本のうち２本しか有効に働いていないのです。

　仮にボルトせん断力（摩擦力）が同じ（P/3）だとすると、プレートのAB間とBC間の引張応力が異なるので伸びも異なり、ボルト締め付け箇所でズレが生じることになってしまいます。

　次に、支圧で力を伝える普通ボルトについて考えます。この場合はボルトがせん断変形するため、上下のプレートに図３のようにズレが生じます。そのズレをδとすると、ボルトのせん断力Qはδに比例します。式で表せば、Q=k・δです。一方、プレートの引っ張り応力Tとプレートの伸びΔlも比例します。Δlをプレートの元の長さで割った歪をεとすると、T=K・εとなります。この応力歪（変形）関係と、A点、A’点、B点での力のつり合いの式からなる連立方程式を解けば、ボルトの剪断力が求まります。中央のボルトにも剪断力が生じますが、両端より小さくなります。

 　摩擦接合では4.5ニュートンにもなるのに実用計算では3ニュートンとしてよいのは何故でしょうか。大丈夫なのでしょうか。上記の計算では、プレートの厚さは無視したモデル化をしていますが、実際には厚さの効果で、中央のボルトにも剪断力が生じます。ただそれは誤差のレベルで、次に述べる理由が重要です。

　鋼材は力に比例して弾性的に変形しますが、降伏点を過ぎると応力は上昇せずに変形が進みます。いわゆる塑性化です。その結果、複数の部材があれば先に降伏した部材が負担する力は増えずに他の部材が代わりに負担します。複数の部材の降伏時の応力が同じなら最終的に均等に分担することになります。この応力再分配が成立するのは、降伏後の変形能力が十分ある場合です。鋼材は変形能力が十分あるから大丈夫だというわけです。通常の許容応力度設計は弾性範囲内で考えますので、許容応力度を超える塑性領域まで考慮するのはおかしいのですが、塑性化を認めないと現実の設計は難しい場合があります。その１例がこの問題です。各ボルトが一様に力を負担するとは限らず、一部に力が集中するような場合、弾性範囲内の設計は困難になります。

　実は、コンクリートのような脆性的材料ではこのような考え方は成り立たない場合があり、現実に地震被害が発生してきました。従って、コンクリートの方が変形能力には特に注意が必要です。このことが強調されだしたのが４０年前の現行耐震設計です。

　また、鋼材は変形能力が大きいとはいえ、最初からバランスよく力を分担させる設計にするに越したことはありません。その意味で引張方向に一列に多数のボルトで接合するような設計では、端部のボルトの負担が大きく、各個撃破的に順番に破断してしまう可能性がないとも限りません

　また鋼材は材料としては変形能力が大きいですが、構造物となった場合は形状的に一気に耐力を失う脆性的崩壊をする場合があります。座屈という不安定現象です。

f:id:shinzor:20210627083540j:plain

 

他者の推理に依存する推理

  • パラドクス

　前回の「帽子色当て問題」では、他者の推理力に依存した推理になっています。そこがどことなく釈然としないところです。問題をもっと単純にしてみても同じです。

２人帽子色当て問題

　白色の帽子２個と赤色の帽子１個から取り出して二人にかぶせる。自分の帽子の色は見えないがもう１人の色は見える。自分の帽子の色を推理して答えなければならない。あなたがもう１人をみたら白色であったので、次のように推理した。

（推理）

自分(B)が赤色と仮定すると、相手(A)は赤色の帽子を見ており、自分(A)が白だと分かる。ところが、相手(A)は答えないので、仮定は間違っており、自分(B)は白色である。

 　この推理は正しいように思えますが、パラドクスになるんですね。

（パラドクスの推理）

自分(B)が白色と仮定すると。相手(A)は自分(B)と同様の状況なので、前述の推理によって相手(A)は、自分(A)が白色と分かる。ところが相手(A)は答えないので仮定は間違っており、自分(B)は赤色である。

 　もっと簡単にいうと、「相手(A)は自分(B)の白をみても推理できない」という前提から、「自分(B)は相手(A)の白を見て推理できる」ことになったので明らかにどこか変です。自分も相手も全く条件は同じなのに、自分には分かるが、相手は分からないという非対称性があります。しかも、相手が分からないことを使って自分だけ分かってしまうのですね。そんな都合のいい話はないから、パラドクスになるのじゃないでしょうか。

 

  • 　推理に必要な情報の非対称性

　結論を言えば、自分には、相手が推理できないという情報があるのに、相手にはないという非対称性があるのだと思います。

　次の文は、２人帽子色当て問題で使う推論で、なりたちます。

 

文１「自分が赤ならば、相手は白である」

 

文１を対偶にしてみれば、自分と相手は全く対称になっています。

 

文２「相手が白でないならば、自分は赤でない」すなわち

　　「相手が赤ならば、自分は白である」

 

　この推論だけで他に情報がなければ、自分の帽子の色は推理できません。では、ほとんど、同じ文ですが、次は成り立つでしょうか。

 

文３　「自分が赤ならば、相手は自分が白だと推理できる」

 

　その対偶は次の通りです。

 

文４「相手が自分を白だと推理できないならば、自分は白である」

 

　文3や文4が成り立つには条件が必要です。帽子の色は客観的な事実ですが、推理は推理力に依存します。従って先ずは完璧な推理が出来るという前提が必要ですが、その前提は認めることにします。それでも、相手が答えないのは「自分の色は分からない」と推理したからなのか、まだ推理中なのか不明です。相手が推理を完了したのか確認しないと、文４は使えません。

　しかし、相手(A)に分からなかったことを確認すれば、Bは自分が白だと推理できます。そして、Bが推理できたことを知った時点でAは推理できなくなります。つまり、与えられる情報に非対称性があるので、Bは推理でき、Aは出来なくなります。これは３人の場合も同じでA、B、Cの順に推理できたかを尋ねていけば、Cは推理できます。すなわち,Aが推理できないと分かれば、BとCの二人とも赤であることはないと推理できます。この時点でCが赤であれば、Bは自分が白だと推理できますが、Cは白なのでできません。次にBが推理できないと分かれば、Cは自分が白だと推理できます。自分以外は全員、推理できないという情報を得て、初めて自分は白だと推理できます。そして、それまでは自分も推理できていなかったということは誰にも教えてはいけません。先を越されます。

  •  他人の気持ちは尋ねなければわからない

　最初の推理の間違いは、自分以外のものが答えないことを、推理が出来ないと勝手に決めつけたことだとと思います。実は、自分は赤なのに相手はまだ考え中かもしれません。２人の場合は、その可能性は少ないですが、逆に相手に先を越されるともう推理できなくなります。そこで、間髪入れずに「白だ」と答えて、帽子をみるとなんと赤です。最初の問題をもう一度見てください。「あなたがもう１人をみたら白色であった」であって、「二人に白い帽子を被せた」とは書いてありません。

 

（4/11 追記）

　最初にパラドクスと書きましたが、「専門的」には、パラドクスとは言わないようです。何の専門なのかよくわかりませんが、この追記の参考にしたスマリヤンのパズル本「この本の名は？」にそう書いてありました。帽子の色あては、単に、推理が間違っているということらしいです。では「専門的」には、パラドクスとはどういうものをいうのかと言うと、真とも偽ともいえない基底性のない文に関わる矛盾らしいです。基底性がないとは、具体的な意味がない（何も情報をもたらさない）ということです。

　文が真か偽を判断するためには、先ずその文の意味を理解する必要があります。「東京は日本の首都である。」と言う文の意味を私は理解していて、東京が日本の首都であることを知っているので、真であると判断できます。ところが「この文は真である。」という文の意味は、この文の真偽に関わることなので、先ずはこの文の真偽を知っていなければ判断できないという循環に陥ります。仮に真と仮定しても偽と仮定しても矛盾は生じないのでパラドクスにはなりませんが、真とも偽ともいえる意味のない文です。一方、「この文は偽である。」も基底性のない文ですが、真と仮定しても偽と仮定しても矛盾が生じるので真とも偽とも言えない意味のないパラドクスになります。

　帽子の色は具体的事実なので、帽子の色を推理したいくつかの文の真偽は定まります。つまり、基底性はあるので、専門的にはパラドクスとは言わず、単に推理が間違っているので矛盾が生じただけです。その間違いについて私の見解を書いたのが本文です。

■ 他者の考えの推測

  • 質問が見当たらない

　ウィキペディアの「眠り姫問題」には、眠り姫が受けた質問はまでは書いてありますが、肝心の読者への質問が書いてありません。ツイッターのやりとりで私は「眠り姫は何と答えたかはわからない。自分が眠り姫の立場なら1/2と答える」と揚げ足とりの注釈をつけたことがあります。我ながらクレーマーみたいでした。常識的に考えれば「あなたが眠り姫の立場なら何と答えるか？」と解釈すればよいだけなので、大人げない態度です。ただ、常識的に解釈することは、先入観で解釈することでもあり、その先入観が混乱を引き起こすのが「眠り姫問題」でもあります。

  • 推理クイズ

　ところで、他者の立場になって考えるといえば、そのタイプの推理クイズがあります。有名なのは、帽子の色当て問題です。

 　白い帽子３つと赤い帽子２つがある。３人にそこから選んだ帽子を被せる。自分の帽子の色は見えないが、他の２人の色は分かる。３人全員に白い帽子を被せて、自分の色を推理させたら、一人が答えたどのように推理したか？

 　この問題は子供の頃に知りましたが、解答を読んでも釈然としませんでした。その推理が、自分以外の者の推理能力を都合よく考えていたからです。自分以外の二人にも適度の推理能力があるけどれも、自分よりは劣っているという何の保証もない前提なので、実際にはそんな推理は出来ないと思いました。

と言いながら、自分が実際にその立場に今なったら「白」と答えます。論理的な推理ではなくヒューリスティックな推測ですので確実に「白」ではなくて「白」の可能性が高いという程度の推測ですが。

私は次のように考えます。

　もし自分の帽子が「赤」ならば、他の２人は「赤」と「白」を見ていることになる。その状況は「白」と「白」を見ている私の状況と違って、多少推理しやすい。なぜなら、その二人にとっては、自分に見えていない二つの「白」と一つの「赤」のうち一つを自分が被っている、つまり「白」である確率は2/3に対して「赤」の確率「1/3」である。ただし、自分が「赤」であれば「白」を被っている者が確実に「白」と分かってしまうので、その可能性は少ない。よって「白」の可能性が非常に高いと推測できるだろう。

　それに対して、「白」二人を見ている私の推測は多少面倒である。見えていない帽子は「白」一つ、「赤」二つなので、私が被っている帽子が「白」である確率は1/3、「赤」である確率は2/3である。しかし、「白」である場合、他の２人にとってその状況は今の私と同じであり、「白」の可能性が高いわけではない。

以上の考察より、出題者が他の２人をえこひいきしたいのでなければ、３人を平等に扱うであろう。故に「白」の可能性が高い。

 　私のヒューリスティックな推測とクイズの回答はよく似ています。ただし、私の推測は出題者の心理を勘案した可能性に過ぎないのに対して、クイズの回答は確定的なものという違いがあります。確定的なのは「論理的」に考えたからですが、仮定条件が非現実的なので信頼性は乏しいです。

　さて、推測にしろ「白」の可能性が高いと判断しましたが、前述のように「白」の確率は1/3です。これは、どのように考えればよいでしょうか。と、問いかけるほどの話ではありませんでした。ヒューリスティックな推測では、他者の推理や出題者の心理を勘案していますが、確率は、残り３つのうち1つということを表しているだけです。コインを投げて帽子の色を決めているなら白の確率は1/3です。確率とはそれだけの意味しかありません。難しい手術の成功確率が○○％と言う場合、患者の生きようとする意欲の類は通常は、反映されていません。実際には、患者の意欲は手術の結果に影響すると思いますが。

多義図形、不可能図形、多義文、不可能文

  • 悲惨なアンケート結果

　「眠り姫問題」は確率の問題としては単純ですが、あいまいな問題文をあいまいと感じさせずに混乱した解釈に引き込む問題だと思います。

　そこで、事前確率を尋ねられていると感じるのか、条件付確率を尋ねられていると感じるのか、それとも、特に意識しないのか、問題の設定によってどのように感じ方が変化するかを確かめようとツイッターのアンケートをしました。しかし、残念ながら、フォロワーがわずかしかいない零細アカウントのためカウンターはゼロのままでした。初めてアンケート機能を使いましたが、フォロワー数が私より二桁ほど多いアカウントの人が使うものですね。恥をかいてしまいました。

　予想では、問1、問2は1/2の回答、問3、問4は1/3の回答が多いと思いましたが確かめることはできませんでした。問１は寝覚め姫視点、問２から４は第三者視点の違いがありますが、基本的に同じ問題を違う表現にしただけです。

　なお、問5、問6は、眠った眠り姫が存在しなくなる異世界バージョンです。「眠り姫問題」では眠っている（コインが表で火曜日）出来事が無視されやすいため、それならと、最初から存在を消してしまったものです。このケースでは、最初から寝覚めている３つの出来事しかありませんので、寝覚めて質問を受けていることは、範囲を狭める条件にはならず、問５は、事前確率を尋ねていることになります。問６は問５と同じ設定で月曜日という条件付き確率を尋ねています。「眠り姫問題」の問３に対応しています。この場合、コインが表の確率は2/3になりますが、別にパラドクスとは感じないと思います。「眠り姫問題」でパラドクスが起こったと混乱するのは、別の問題である問1から問4と問5、問6が頭のなかで区別できずに混じってしまったためでしょう。

  • いくつかのタイプの確率問題

　確率は０～１の分数です。確率の問題は、言語で表現した設定から、分子と分母をどのような数にするのが妥当かを問いかけます。言語表現の解釈が明確に定まる場合でも、誤解釈はあり、その代表例が「モンティ・ホール問題」です。誤解釈に気づくのが難しい場合、大論争になりますが、いずれ決着します。

　また、解釈が定まらず、それが分かりやすい場合は、あいまいな問題だと誰もが考えるので、問題の不備とされて終りです。分かりにくい場合は違う解釈をする者の間で大論争になります。この場合はそれぞれの立場の者は自分の解釈に自信があるので、別の立場の解釈もあることに気づかないと論争は決着しません。どちらかが間違っているわけではないからです。違う問題について考えているのに同じ問題だとお互いに勘違いしている状況です。設定に不備のある「もう一人も女の子の確率問題」がこの例です。

　以上とはまた一風変わった「眠り姫問題」は、あいまいな問題の異なる解釈が一人の人間の頭の中でせめぎあう面白い例だと思います。どちらかの立場に決めてしまえばスッキリしますが、なかなかそうは割り切れない非現実的な設定になっています。二つの立場は両立しませんのでパラドクスに思えます。現実的な設定にするとどちらかの立場に落ち着くのでパラドクス感は消えますが、あいまいな設定が残っていれば、違う立場との論争は続きます。

　アンケート問１は「眠り姫問題」とほぼ同じ非現実設定で、なおかつ眠り姫視点なのでパラドクス感が強くなります。問２は第三者視点なので問１とは違う問題だと感じる人もいるようですが、寝覚めた眠り姫と第三者に与えられた情報は全く同じです。問３と問４は現実的設定でパラドクス感はありませんが、違う立場での決着のつかない論争はあるかもしれません。

  • 多義図形、不可能図形

　錯視の一種に「多義図形」、「不可能図形」があります。

www.psy.ritsumei.ac.jp

www.psy.ritsumei.ac.jp

　多義図形の中でも、だまし絵タイプでは片方しか見えない場合があって、別の見え方をする人と論争になったりします。不可能図形はパラドクスのような不思議な印象があります。この言語版が「眠り姫問題」ではないでしょうか。立体を平面上に表現すると情報が不足するので二通りの解釈ができるように、現実の出来事を言葉で表現すると二通りの解釈が可能になる場合があります。日常会話でも「そういう意味じゃなくて」という場面はよくあり、お笑いのネタにもなっています。また不可能図形は先入観のため不可能に見えるのですが、実際に立体として作ることもできます。これに対応しているのが問6です。下記のリンク先の説明を参照してください。不可能に見えるのは「連続している」、「平面である」、「直角である」と勝手な先入観があるからで、「非連続」、「局面曲面」、「非直角」にしてしまえば不可能図形立体が出来上がります。

不可能立体の進化

 

「眠り姫問題」2021/04/01 時点でのまとめ

  • 　結論（多分）

　３月１５日に「現時点のまとめ」をしました。「1/3」の答えが妥当というものでした。その後、nananana0110さんから貴重なコメントを頂き、「1/3」と「1/2」の両方の解釈が可能なあいまいな問題と思うようになりました。それでも、数日前までは、問題の設定を使うのなら「1/3」と考えるのが自然だと思っていました。しかし、「1/2」と考える人がどのように感じているか、自分の当初の直観で「1/2」と思ったのは何故か、を思いだし、さらに「1/3」に意見を変えた理由を考えてみると「自然」とは感覚的なもので、人によって感じ方が違い、両者に優劣などないというところに落ち着いてきました。どうとでも解釈できるあいまいな問題だという結論です。

  • 　それぞれの解釈

　それぞれの解釈をまとめます。まず、前提の確率を考える「出来事」は次の４つです。

①表がでた後の月曜日に寝覚め、質問を受ける。

②表がでた後の火曜日に寝ていて、質問は受けない。

③裏がでた後の月曜日に寝覚め、質問を受ける。

④裏がでた後の火曜日に寝覚め、質問を受ける。

　これらが実験中の総ての可能性で、また、これらを同等と考えて、それぞれの確率は「1/4」とします。

　「1/2」派は、次のように考えます。問2は「さあ、あなたは目覚めた。表 である確率は？」であり、「さあ、あなたは目覚めた」は単なる今の状態を述べているだけで、条件ではないのだから、

　　(①＋②)÷(①＋②＋③＋④)=1/2

である。つまり事前確率を尋ねられたと解釈します。

　これに対して、「1/3」派は、問2は「さあ、あなたは目覚めた。表 である確率は？」であり、目覚めた状態での確率を尋ねているのだから、

　　①÷(①＋③＋④)=1/3

である。つまり、目覚めたという条件付き確率を尋ねられたと解釈します。

　では、問3「さあ、あなたは目覚めた。今は月曜日である。表である確率は？」については、各派はどのように考えるでしょうか。

　「1/2」派は、問2の「さあ、あなたは目覚めた」が確率を出す条件とは考えずに単なる今の状態を述べているだけと考えたのですから、問3も同じように事前確率を問われていると解釈して、

　　(①＋②)÷(①＋②＋③＋④)=1/2

と答えるのが首尾一貫します。これでなんの問題もパラドックスも生じません。

　これに対して「1/3」派は、月曜日という条件付き確率を尋ねられたと解釈し、

　　①÷（①＋③）=1/2

と答えます。「1/2」派と考え方は違いますが、結果は同じです。なお、「眠り姫問題」ではたまたま同じだけで、一般的には違ってきます。

　また仮に「1/2」派が、問23は条件付き確率と解釈しても、一貫性に欠けますが、違う質問ですから別にいいでしょう。

　なにもパラドックスはないのにあるように感じるのは、何故でしょう。私の場合は、問2を事前確率と解釈して（自覚はなかったが）1/2としたのに、

　①÷（①＋③＋④）＝1/2

　だと勘違いしていました。これだと①は1/2となって、問3の答えが2/3になるのでパラドクスめいてきます。この勘違いが起こるのは②は最初から存在しないような気がするからです。意識がない姫は存在しないと考えてしまうわけです。同時に「目覚め」も条件とは感じなくなります。目覚めている状態しか存在しないわけですから。

　私はよく知りませんが、公理論的確率論では、①～④の確率を1/4としなければならない理由はないようです。①=1/2、②=0、③＝④＝1/4　としても構いません。ただし、それは私たちが住む現実世界とは違い、眠ると存在が消えてしまう想像上の異世界なので、月曜日という条件付き確率は2/3になります。

　勘違いしなければ、どのように解釈してもパラドクスにはなりません。勘違いのパラドクスを解決するため、難解（アドホック）な理屈が考えられているようですが、そんな必要はないと思います。

  • 眠っているという条件付き確率

　眠っているという条件付き確率もありますが、残念なことに、眠っている眠り姫に質問はできません。そこで、夢の中に侵入して質問するSFっぽいことを考えたりしましたが、実験前に次のような質問をすればほぼ同じことができます。

問４「さあ、これから実験を行う。実験中、あなたが眠っている時に表である確率は？」

　また、次の質問も考えられます。

問５「さあ、これから実験を行う。実験中、あなたが寝覚めている時に表である確率は？」

　これと、実験中に行う次の質問は同じでしょうか、違うでしょうか。

問２「さあ、あなたは目覚めた。表 である確率は？」

 

 （4/3 追記）

　条件付確率の問題であることを明確にする設定はないかと考えていたら、遅読猫さんのブログに書いてありました。（今は消えていますが）

　最初にコイン投げを録画しておいて、寝覚めた眠り姫に録画のコインの表の確率を尋ねるというものです。賭けバージョンと同じですが、こちらの方が問題文としてスッキリしています。「表の録画は1回、裏の録画は2回見せられるので・・・」と考えやすいです。